
 
Spherical coordinates, also called spherical polar coordinates (Walton 1967, Arfken 1985), are a system of curvilinear
coordinates that are natural for describing positions on a sphere or spheroid.
Define  to be the azimuthal angle in the to be the azimuthal angle in the
 -plane
from the x-axis with -plane
from the x-axis with  (denoted
(denoted 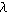 when referred to as
the longitude), when referred to as
the longitude), 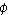 to be the polar angle from the z-axis with to be the polar angle from the z-axis with  (colatitude, equal to
(colatitude, equal to 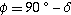 where
where  is the latitude),
and is the latitude),
and  to be distance (radius) from a point to the origin.
This is the convention commonly used in mathematics. to be distance (radius) from a point to the origin.
This is the convention commonly used in mathematics.
In this work, following the mathematics convention, the symbols for the radial, azimuth, and zenith
coordinates are taken as 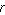 , , 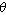 , and , and  , respectively.
Note that this definition provides a logical extension of the usual polar coordinates notation, with , respectively.
Note that this definition provides a logical extension of the usual polar coordinates notation, with  remaining the
angle in the remaining the
angle in the  -plane and -plane and  becoming the
angle out of that plane. The sole exception to this convention in this work is
in spherical harmonics, where
the convention used in the physics literature is retained (resulting, it is hoped,
in a bit less confusion than a foolish rigorous consistency might engender). becoming the
angle out of that plane. The sole exception to this convention in this work is
in spherical harmonics, where
the convention used in the physics literature is retained (resulting, it is hoped,
in a bit less confusion than a foolish rigorous consistency might engender).
Unfortunately, the convention in which the symbols  and and  are reversed
is also frequently used, especially in physics. The symbol are reversed
is also frequently used, especially in physics. The symbol  is sometimes
also used in place of is sometimes
also used in place of  , and , and  and and  instead of instead of  . The following table summarizes a number of conventions
used by various authors; be very careful when consulting the literature. . The following table summarizes a number of conventions
used by various authors; be very careful when consulting the literature.
| (radial, azimuthal, polar) | reference |  | this work, Zwillinger (1985, pp. 297-298) |  | Beyer
(1987, p. 212) |  | Korn and Korn (1968, p. 60) |  | Misner
et al. (1973, p. 205) | | (Rr, Pphi,
Ttheta) | SetCoordinates[Spherical[r, Ttheta, Pphi]]
in the Mathematica
add-on package Calculus`VectorAnalysis` (which can be loaded with the command
<<Calculus`) | 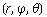 | Arfken (1985, p. 102) |  | Moon and Spencer (1988, p. 24) |
The spherical coordinates  are
related to the Cartesian coordinates are
related to the Cartesian coordinates 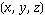 by by
where 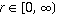 , ,  ,
and ,
and ![phi in [0,pi]](SphericalCoordinates_files/inline42.gif) , and the inverse tangent must be suitably defined to take the correct
quadrant of , and the inverse tangent must be suitably defined to take the correct
quadrant of  into account. into account.
In terms of Cartesian coordinates,
The scale factors are
so the metric coefficients are
The line element is
 |
(13)
|
the area element
 |
(14)
|
and the volume element
 |
(15)
|
The Jacobian is
 |
(16)
|
The position vector is
![r=[rcosthetasinphi; rsinthetasinphi; rcosphi],](SphericalCoordinates_files/equation5.gif) |
(17)
|
so the unit vectors are
Derivatives of the unit vectors
are
The gradient is
 |
(33)
|
and its components are
(Misner et al. 1973, p. 213, who however use the notation convention  ). ).
The Christoffel symbols of the second kind in the definition of Misner et al. (1973, p.
209) are given by
(Misner et al. 1973, p. 213, who however use the notation convention  ). The Christoffel symbols of the second kind in the definition of
Arfken (1985) are given by ). The Christoffel symbols of the second kind in the definition of
Arfken (1985) are given by
(Walton 1967; Moon and Spencer 1988, p. 25a; both of whom however use the notation convention  ). ).
The divergence is
 |
(49)
|
or, in vector notation,
The covariant derivatives
are given by
 |
(52)
|
so
The commutation coefficients
are given by
![c_(alphabeta)^mue^->_mu==[e^->_alpha,e^->_beta]==del _alphae^->_beta-del _betae^->_alpha](SphericalCoordinates_files/equation9.gif) |
(62)
|
![[r^^,r^^]==[theta^^,theta^^]==[phi^^,phi^^]==0,](SphericalCoordinates_files/equation10.gif) |
(63)
|
so  ,
where ,
where  . .
![[r^^,theta^^]==-[theta^^,r^^]==del _rtheta^^-del _thetar^^==0-1/rtheta^^==-1/rtheta^^,](SphericalCoordinates_files/equation11.gif) |
(64)
|
so  , ,
 . .
![[r^^,phi^^]==-[phi^^,r^^]==0-1/rphi^^==-1/rphi^^,](SphericalCoordinates_files/equation12.gif) |
(65)
|
so  . .
![[theta^^,phi^^]==-[phi^^,theta^^]==1/rcotphitheta^^-0==1/rcotphitheta^^,](SphericalCoordinates_files/equation13.gif) |
(66)
|
so
 |
(67)
|
Summarizing,
Time derivatives of the position
vector are
The speed is therefore given by
 |
(74)
|
The acceleration is
Plugging these in gives
but
so
Time derivatives of the unit vectors are
The curl is
![del xF==1/(rsinphi)[partial/(partialphi)(sinphiF_theta)-(partialF_phi)/(partialtheta)]r^^+1/r[1/(sinphi)(partialF_r)/(partialtheta)-partial/(partialr)(rF_theta)]phi^^+1/r[partial/(partialr)(rF_phi)-(partialF_r)/(partialphi)]theta^^.](SphericalCoordinates_files/equation16.gif) |
(89)
|
The Laplacian is
The vector Laplacian in spherical
coordinates is given by
![del ^2v==[1/r(partial^2(rv_r))/(partialr^2)+1/(r^2)(partial^2v_r)/(partialtheta^2)+1/(r^2sin^2theta)(partial^2v_r)/(partialphi^2)+(cottheta)/(r^2)(partialv_r)/(partialtheta)-2/(r^2)(partialv_theta)/(partialtheta)-2/(r^2sintheta)(partialv_phi)/(partialphi)-(2v_r)/(r^2)-(2cottheta)/(r^2)v_theta
1/r(partial^2(rv_(theta)))/(partialr^2)+1/(r^2)(partial^2v_(theta))/(partialtheta^2)+1/(r^2sin^2theta)(partial^2v_(theta))/(partialphi^2)+(cottheta)/(r^2)(partialv_(theta))/(partialtheta)-2/(r^2)(cottheta)/(sintheta)(partialv_(phi))/(partialphi)+2/(r^2)(partialv_r)/(partialtheta)-(v_(theta))/(r^2sin^2theta)
1/r(partial^2(rv_(phi)))/(partialr^2)+1/(r^2)(partial^2v_(phi))/(partialtheta^2)+1/(r^2sin^2theta)(partial^2v_(phi))/(partialphi^2)+(cottheta)/(r^2)(partialv_(phi))/(partialtheta)+2/(r^2sintheta)(partialv_r)/(partialphi)+(2cottheta)/(r^2sintheta)(partialv_(theta))/(partialphi)-(v_(phi))/(r^2sin^2theta) ].](SphericalCoordinates_files/equation17.gif) |
(93)
|
To express partial derivatives with respect to Cartesian axes in terms of partial
derivatives of the spherical coordinates,
Upon inversion, the result is
![[dr; dtheta; dphi]==[costhetasinphi sinthetasinphi cosphi; -(sintheta)/(rsinphi) (costheta)/(rsinphi) 0; (costhetacosphi)/r (sinthetacosphi)/r -(sinphi)/r][dx; dy; dz].](SphericalCoordinates_files/equation18.gif) |
(97)
|
The Cartesian partial derivatives
in spherical coordinates are therefore
(Gasiorowicz 1974, pp. 167-168; Arfken 1985, p. 108).
The Helmholtz differential
equation is separable in spherical coordinates.

Arfken, G. "Spherical Polar Coordinates." §2.5 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL:
Academic Press, pp. 102-111, 1985.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton,
FL: CRC Press, 1987.
Gasiorowicz, S. Quantum Physics. New York: Wiley, 1974.
Korn, G. A. and Korn, T. M. Mathematical Handbook for Scientists and Engineers. New
York: McGraw-Hill, 1968.
Misner, C. W.; Thorne, K. S.; and Wheeler, J. A. Gravitation. San Francisco, CA: W. H. Freeman, 1973.
Moon, P. and Spencer, D. E. "Spherical Coordinates  ."
Table 1.05 in Field Theory Handbook, Including Coordinate Systems, Differential
Equations, and Their Solutions, 2nd ed. New York: Springer-Verlag, pp. 24-27,
1988. ."
Table 1.05 in Field Theory Handbook, Including Coordinate Systems, Differential
Equations, and Their Solutions, 2nd ed. New York: Springer-Verlag, pp. 24-27,
1988.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill,
p. 658, 1953.
Walton, J. J. "Tensor Calculations on Computer: Appendix." Comm. ACM 10,
183-186, 1967.
Zwillinger, D. (Ed.). "Spherical Coordinates in Space." §4.9.3 in CRC Standard Mathematical Tables and Formulae. Boca Raton,
FL: CRC Press, pp. 297-298, 1995.
|


